
📝문제 설명
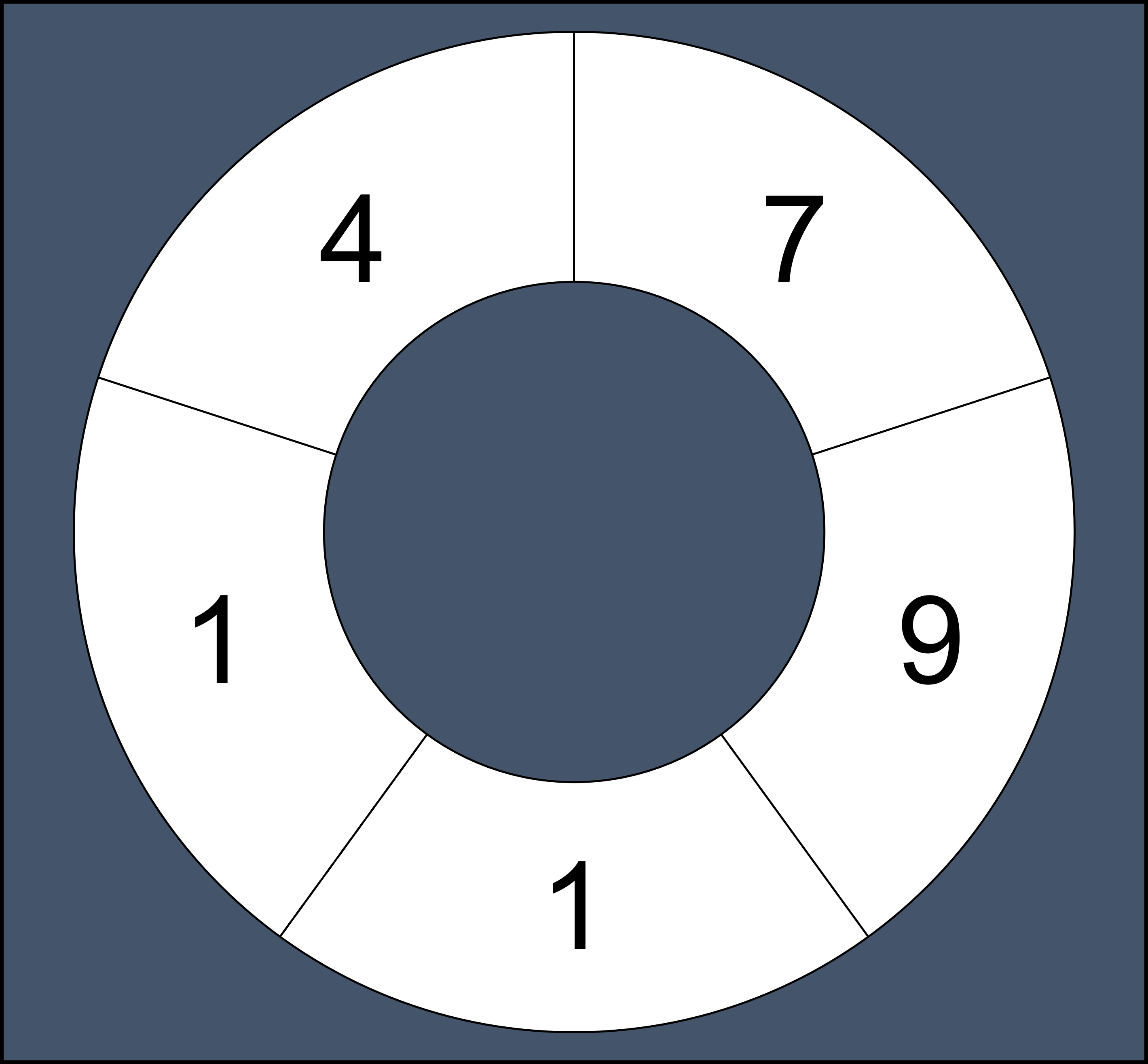

합을 구하는 길이가 1인 연속 부분 수열 [1, 4, 7, 9] 4가지
합을 구하는 길이가 2인 연속 부분 수열 [2, 5, 10, 11, 16] 5가지
합을 구하는 길이가 3인 연속 부분 수열 [6, 11, 12, 17, 20] 5가지
합을 구하는 길이가 4인 연속 부분 수열 [13, 15, 18, 21] 4가지
합을 구하는 길이가 5인 연속 부분 수열 [22] 1가지
이들 중 중복되는 값을 제외하고 총 몇가지 인지 반환!
중복값 제외면 자료구조는 Set을 사용하면 된다.
📢입출력 예시

✏️문제 풀이
import java.util.*;
class Solution {
public int solution(int[] elements) {
Set<Integer> mySet = new HashSet<>();
for(int i=0; i<elements.length; i++){
int sum = 0;
for(int j=0; j<elements.length; j++){
sum += elements[(i+j) % elements.length];
mySet.add(sum);
}
}
return mySet.size();
}
}
아래에 설명한 대로 처음에는 슬라이딩 윈도우를 사용하여 윈도우 크기마다 합을 구해줬고 Set에 담아 저장했다.
하지만 3중반복문이라 O(n^3)로 시간초과가 발생하였다.
윈도우 크기말고 현재 인덱스 값에서 길이만큼까지 계속 더하면 어떨까 생각했고 범위가 넘어가면 %를 사용해 첫 인덱스로 넘어가게 만들었다.
그림으로 설명하자면



7, 7+9, 7+9+1, 7+9+1+1, 7+9+1+1+4
9, 9+1, 9+1+1, 9+1+1+4, 9+1+1+4+7
1, 1+1, 1+1+4, 1+1+4+7, 1+1+4+7+9
이런식으로 슬라이딩 윈도우와의 경우의 수는 똑같지만 계산 방식을 다르게 했다.
💡새로 알게된 점
import java.util.*;
class Solution {
public int solution(int[] elements) {
Set<Integer> mySet = new HashSet<>();
//슬라이딩 회수
for(int i=0; i<=elements.length; i++){
// 윈도우 시작 위치
for(int j=0; j<elements.length; i++){
int sum = 0;
// 윈도우 내 합 계산
for(int k=j; k<i+j; k++){
sum += elements[k%elements.length];
}
mySet.add(sum);
}
}
return mySet.size();
}
}
처음에는 슬라이딩 윈도우 기법을 사용해서 윈도우 크기를 늘리면서 계산하니 3중 반복문이 나왔고
시간초과가 나서 다른 기법을 생각해보았다.
다른 풀이를 찾아봤는데 회전배열 문제에선 길이를 2배로 늘려놓고 하는 기법도 있더라,,
'📖Algorithm > Simulation, Math' 카테고리의 다른 글
| JAVA [Algorithm] - 백준 1193 분수 찾기 (0) | 2024.12.19 |
|---|---|
| 자바 [Programmers] 2단계 - 점프와 순간이동 (0) | 2024.12.03 |
| 자바 [Programmers] 2단계 - JadenCase 문자열 만들기 (0) | 2024.11.28 |
| 자바 [Programmers] 2단계 - 이진 변환 반복하기 (0) | 2024.11.28 |
| 자바 [Programmers] 2단계 - 다음 큰 숫자 (0) | 2024.11.28 |

