📝문제 설명

📢입출력 예시

✏️문제 풀이
백트래킹의 대표적인 문제로 백트래킹의 근본 문제라고 볼 수 있다.
N-Queen 문제 이해가 잘 안된다면 밑의 링크를 통해 어떤 방식으로 접근해야 되는지 알아보자.
https://namu.wiki/w/%EC%97%AC%EB%8D%9F%20%ED%80%B8%20%EB%AC%B8%EC%A0%9C
여덟 퀸 문제
여덟 퀸 문제는 1848년 막스 베첼이 처음으로 제안한 퍼즐 문제로, 수학 과 컴퓨터과학 에서 알고리즘 문제
namu.wiki
우리가 고려해야 될 점은 단 2가지이다.
1. 재귀함수를 어떻게 호출할 것인가. (매개변수 설정)
2. 같은 행,열, 대각선에 있는지 어떻게 판단할 것인가.
내가 보기엔 이 두가지만 해결하면 문제를 풀 수 있을 것 같았다.
사실 이 문제는 내 지식 100%를 사용하여 풀지 않았고 다른 풀이들을 참고해서 풀었다.
하지만 해설은 나만의 방법으로 해보겠다.
먼저 N=4인 경우로 풀이를 해 보겠다.

1차원 배열로 N 크기 만큼 int형 배열을 선언한다.
인덱스에 들어갈 값은 행의 번호
인덱스 값은 열의 번호라고 생각하면 된다.
이를 2차원 배열로 시각화를 하면
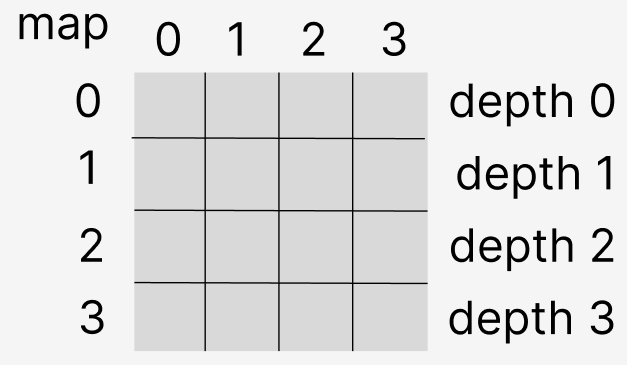
위와 같은 모양이 되며
예를 들어 1차원 배열에 값이 아래와 같이 들어가게 된다면
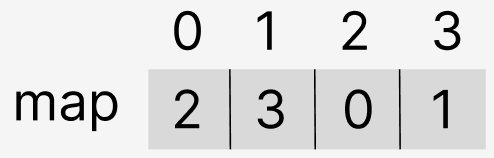
map[0] = 2 => [2,0]
map[1] = 3 => [3,1]
map[2] = 0 => [2,0]
map[3] = 1 => [1,3]
2차원 배열로는 아래와 같이 시각화 할 수 있다.

전체 코드를 본 후 메서드 별로 설명을 해 보겠다.
package Baekjoon.BackTracking;
import java.util.Scanner;
public class Baek9663 {
static int[] map;
static boolean[] visited;
static int N, count;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
N = scanner.nextInt();
map = new int[N];
visited = new boolean[N];
backTracking(0);
System.out.println(count);
}
private static void backTracking(int depth){
if(depth == N){
count++;
return;
}
for(int i=0; i<N; i++){
map[depth] = i;
if(checkPossible(depth)){
backTracking(depth+1);
}
}
}
private static boolean checkPossible(int col){
for(int i=0; i<col; i++){
//같은 행에 있을 경우
if(map[i] == map[col]){
return false;
}
//대각선에 위치할 경우
else if(Math.abs(col-i) == Math.abs(map[col] - map[i])){
return false;
}
}
return true;
}
}
1. backTracking 함수
private static void backTracking(int depth){
if(depth == N){
count++;
return;
}
for(int i=0; i<N; i++){
map[depth] = i;
if(checkPossible(depth)){
backTracking(depth+1);
}
}
}
depth는 행의 값를 뜻하며 depth 인덱스에 들어갈 값은 열의 값을 의미한다라는 것을 잊지 말자
N 크기만큼 반복문으로 depth가 0일때 즉, 2차원 배열에서 첫 행에 값 넣어야 한다.
1. depth = 0, i = 0

위와 같이 저장된다.
checkPossible에서는 어차피 매개변수 값이 0이므로 true가 나오게 되며 다음 재귀함수를 호출하게 된다.
2. depth = 1, i = 0

위와 같이 저장되며 같은 열, 행에 있는지 검사를 해야한다.
2. checkPossible 함수
private static boolean checkPossible(int col){
for(int i=0; i<col; i++){
//같은 열에 있을 경우
if(map[i] == map[col]){
return false;
}
//대각선에 위치할 경우
else if(Math.abs(col-i) == Math.abs(map[col] - map[i])){
return false;
}
}
return true;
}
col 값은 1로 들어왔고 col보다 작을 때까지 반복문을 수행한다.
현재 map[0] = 0, map[1] = 0이다.
인덱스 안에 저장된 값은 열 값을 의미한다고 했으니 0값이 중복되면 안된다.
따라서 위 경우는 같은 열에 있다고 본다.
3. depth = 1, i = 1

checkPossible에서 배열의 값이 동일하지 않으니 같은 열에 있다는 것은 아니고
이제 대각선에 있다는 것을 판단해줘야 한다.
두 점이 대각선 방향에 있는지 확인하는 방법은 간단한 수학 공식을 활용한다.
(x1, y1)와 (x2, y2)가 존재한다면
: 오른쪽 위 대각선 방향으로 같은 거리에 있음.
: 오른쪽 아래 대각선 방향으로 같은 거리에 있음.
우리는 왼쪽 위,아래 오른쪽 위,아래 둘다 확인해야 하기 때문에 절대값을 사용해서 판단한다.
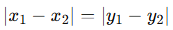
위와 같이 판단하면 될 것이다.
if(Math.abs(col-i) == Math.abs(map[col] - map[i])){
return false;
}(x1, y1) (x2, y2)를 우리가 정의한 변수 값으로 치환하면 아래와 같고
(i, map[i]) (col, map[col])
이를 공식으로 적용시킨다.
💡새로 알게된 점
백트래킹은 재귀함수를 어떻게 호출하고 호출 했을 때 다음 값을 어떻게 처리할지에 대한 고민만 많이 해보자
'📖Algorithm > BackTracking' 카테고리의 다른 글
| JAVA [Algorithm] - 백준 14888 연산자 끼워 넣기 (0) | 2025.01.08 |
|---|---|
| JAVA [Algorithm] - 백준 14889 스타트와 링크 (0) | 2025.01.08 |
| JAVA [Algorithm] - 백준 15650 N과 M (2) (0) | 2025.01.06 |
| JAVA [Algorithm] - 백준 15649 N과 M (1) (0) | 2025.01.06 |

