1.1 시간 복잡도 표기법 알아보기
시간 복잡도란?
- 알고리즘에서 시간 복잡도는 주어진 문제를 해결하기 위한 연산 횟수를 말한다.
- 일반적으로 수행시간 1억번의 연산을 1초의 시간으로 간주하여 예측한다.
시간 복잡도 정의하기
- Big-Omega(Ω) : 최선일 때(Best Case)의 연산 횟수를 나타낸 표기법
- Big-Theta(θ) : 보통일 때(Average Case)의 연산 횟수를 나타낸 표기법
- Big-O : 최악일 때(Worst Case)의 연산 횟수를 나타낸 표기법
코딩테스트에서의 시간 복잡도 사용 유형은?
- 코딩테스트에서는 Big-O 표기법을 기준으로 수행 시간을 계산하는 것이 좋다.
- 다양한 테스트 케이스를 수행해 모든 케이스를 통과해야만 합격으로 판단하므로 시간 복잡도를 판단할 때는 최학일 때(Worst Case)를 염두에 둬야 한다.

1.2 시간 복잡도 활용하기
백준 2750번 수 정렬하기
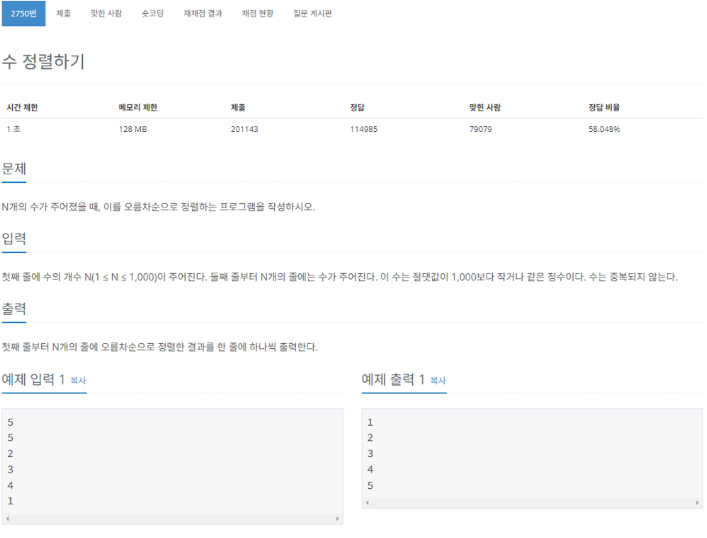
시간 제한이 2초이므로 이 조건을 만족하려면 2억 번 이하의 연산 횟수로 문제를 해결해야 한다.
따라서 주어진 시간 제한과 데이터 크기를 바탕으로 어떤 정렬 알고리즘을 사용할 것인지 판단할 수 있다.
연산 횟수 계산 방법
- 연산 횟수 = 알고리즘 시간 복잡도 x 데이터 크기
알고리즘 적합성 평가
- 버블 정렬 = O(N^2) = (1,000,000)^2 = 1,000,000,000,000 > 200,000,000 ⇒ 부적합 알고리즘
- 병합 정렬 = O(nlogn) = 1,000,000 log(1,000,000) = 약 20,000,000 < 200,000,000 ⇒ 적합 알고리즘
시간 복잡도를 바탕으로 코드 로직 개선하기
시간 복잡도 도출 기준
- 상수는 시간 복잡도 계산에서 제외한다.
연산 횟수가 N인 경우
public class test {
public static void main(String[] args){
int n = 100000;
int cnt = 0;
for(int i=0; i< n; i++){
System.out.println("연산 횟수 :" + cnt++);
}
}
}
연산 횟수가 3N인 경우
public class test {
public static void main(String[] args){
int n = 100000;
int cnt = 0;
for(int i=0; i< n; i++){
System.out.println("연산 횟수 :" + cnt++);
}
for(int i=0; i< n; i++){
System.out.println("연산 횟수 :" + cnt++);
}
for(int i=0; i< n; i++){
System.out.println("연산 횟수 :" + cnt++);
}
}
}
연산횟수가 N과 3N이 있다. 언뜻 생각하면 큰 차이인 것 같지만 코딩테스트에선 상수를 무시하므로 두 코드 모두 시간 복잡도 O(n)으로 같다.
- 가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준이 된다.
연산 횟수가 N^2인 경우
public class test {
public static void main(String[] args){
int n = 100000;
int cnt = 0;
for(int i=0; i<n; i++){
for(int j=0; j<n;j++) {
System.out.println("연산 횟수 :" + cnt++);
}
}
}
}
시간 복잡도는 가장 많이 중첩된 반복문을 기준으로 도출하므로 이 코드에서는 이중 for문이 전체 코드의 시간 복잡도 기준이 된다. 반약 뒤에 일단 for문이 10개 더 있더라도 도출 원리의 기준에 따라서 N^2으로 유지된다.
'📖Algorithm > Library' 카테고리의 다른 글
| 자바 [Algorithm] 알고리즘 - 구간 합 (0) | 2024.03.19 |
|---|---|
| 자바 [Algorithm] 자료구조 - 배열과 리스트 (0) | 2024.03.19 |
| 자바 [Algorithm] 디버깅 (0) | 2024.03.19 |
| 자바 [JAVA] - 문자열을 정수로 변환 (0) | 2024.02.15 |
| 자바 [JAVA] - 문자열 대소문자로 변환하는 방법 toLowerCase, toUpperCase (0) | 2024.02.14 |
